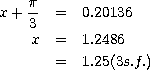compound-angle

1 Compound Angle Formulae

1.1 Learning Objectives

Knowledge and use of formulae for sinA ± B,cosA ± B,tanA ± B; double angle formulae for sin2h,cos2h,tan2h.

Solution of equations, eg 3sin2h = cosh and cosxsin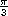![p

3](compound-angle0x.gif) + sinxcos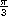![p

3](compound-angle1x.gif) = 0.2, etc. General solutions will not be expected. Solutions may be required in degrees or radians.

1.2 Compound Angles

There are two basic methods to prove these formulae. One is by using complex numbers and we have not yet covered those in this course. It also involves a certain amount of algebraic manipulation, so instead we examine the following short geometric proof in the figure. This proof is valid for small angles only, but illustrates the equation well.

PIC
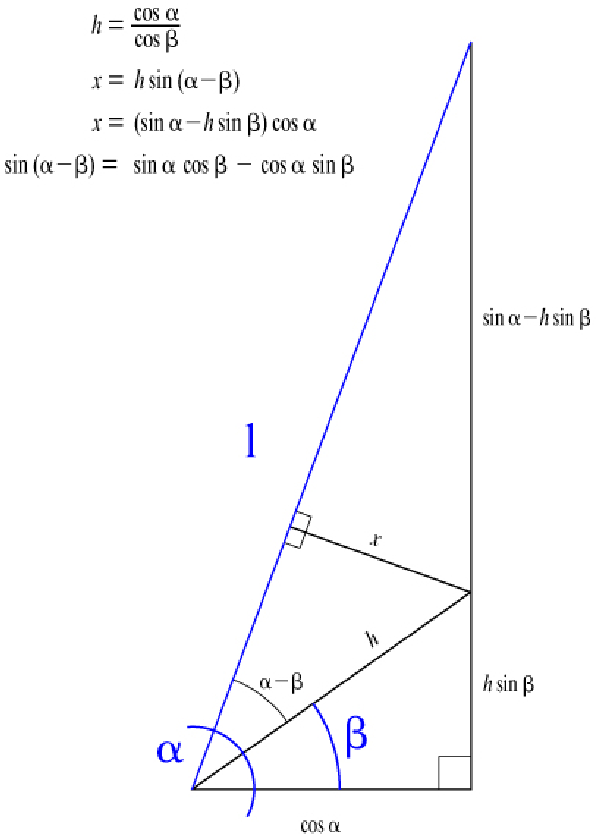
| Figure 1: | Diagram by DeborahSmiley of Ivyworks
---|---

The proof of the subtraction formula for cos can be developed by making the opposite length 1 and the other of the two possible angles b. Then the addition formulae are derived by allowing -b in place of b and using the evenness/oddness of the functions. Finally, tan formulae are found by combining and rearranging sin and cos. To summarise:

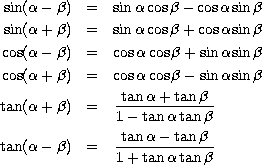
![ sin(a- b) = sina cosb - cosasinb

sin(a+ b) = sina cosb + cosasinb

cos(a- b) = cosa cosb + sin asinb

cos(a+ b) = cosa cosb- sin asinb

           tana-+-tanb--

tan(a+ b) = 1- tanatan b

           tana - tanb

tan(a- b) = 1+-tanatan-b-

](compound-angle3x.gif)

1.3 Double Angles

It is a simple matter of letting a = b = h in the addition formulae to obtain:

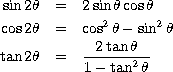
![sin 2h = 2sinhcosh

cos2h = cos2h- sin2 h

        2tanh

tan 2h = 1---tan2h-

](compound-angle4x.gif)

1.4 Solving Equations

Worked examples. First one:

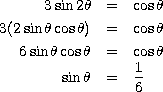
![ 3sin2h = cosh

3(2sinhcosh) = cosh

6sin hcosh = cosh

             1
    sin h  =  6

](compound-angle5x.gif)

Fire up a calculator:

octave:1> asin(1/6)
ans = 0.16745

This answer is in radians.

Second one:

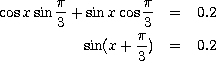
![cosxsin p-+ sin xcos p = 0.2

   3          3
       sin\(x+ p-\) =   0.2
             3

](compound-angle6x.gif)

Fire up the calculator:

octave:4> asin(0.2)
ans = 0.20136
octave:5> asin(0.2)+(pi/3)
ans = 1.2486

So:

![x + p- = 0.20136

3
x  =  1.2486
   =  1.25\(3s.f.\)

](compound-angle7x.gif)